1.1.6 Условные выражения и предикаты

Выразительная сила того класса процедур, которые мы уже научились определять, очень ограничена, поскольку пока что у нас нет способа производить проверки и выполнять различные операции в зависимости от результата проверки. Например, мы неспособны определить процедуру, вычисляющую модуль числа, проверяя, положительное ли это число, отрицательное или ноль, и предпринимая различные действия в соответствии с правилом

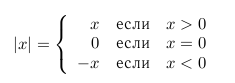
Такая конструкция называется разбором случаев (case analysis). В Лиспе существует особая форма для обозначения такого разбора случаев.Она называется cond (от английского слова conditional, «условный») и используется так:

Общая форма условного выражения такова:

Она состоит из символа cond, за которым следуют заключенные в скобки пары выражений ((p) (e)), называемых ветвями (clauses). В каждой из этих пар первое выражение — предикат (predicate), то есть выражение, значение которого интерпретируется как истина или ложь.

Условные выражения вычисляются так: сначала вычисляется предикат (p1). Если его значением является ложь, вычисляется (p2). Если значение (p2) также ложь, вычисляется (p3). Этот процесс продолжается до тех пор, пока не найдется предикат, значением которого будет истина, и в этом случае интерпретатор возвращает значение соответствующего выражения-следствия (consequent expression) в качестве значения всего условного выражения. Если ни один из (p) ни окажется истинным, значение условного выражения не определено.

Словом предикат называют процедуры, которые возвращают истину или ложь, а также выражения, которые имеют значением истину или ложь. Процедура вычисления модуля использует элементарные предикаты <,= и >. Они принимают в качестве аргументов по два числа и, проверив, меньше ли первое из них второго, равно ему или больше, возвращают в зависимости от этого истину или ложь.

Можно написать процедуру вычисления модуля и так:

(define (abs x)

(cond ((< x 0) (- x))

(else x)))

что на русском языке можно было бы выразить следующим образом: «если x меньше нуля, вернуть −x; иначе вернуть x». Else — специальный символ, который в заключительной ветви cond можно использовать на месте hpi. Это заставляет cond вернуть в

качестве значения значение соответствующего hei в случае, если все предыдущие ветви были пропущены. На самом деле, здесь на месте hpi можно было бы использовать любое выражение, которое всегда имеет значение истина.

Вот еще один способ написать процедуру вычисления модуля:

(define (abs x)

(if (< x 0)

(- x)

x))

Здесь употребляется особая форма if, ограниченный вид условного выражения. Его можно использовать при разборе случаев, когда есть ровно два возможных исхода. Общая форма выражения if такова:

(if (предикат) (следствие) (альтернатива))

Чтобы вычислить выражение if, интерпретатор сначала вычисляет его hпредикатi. Если (предикат) дает истинное значение, интерпретатор вычисляет (следствие) и возвращает его значение. В противном случае он вычисляет hальтернативуi и возвращает ее значение 19.

В дополнение к элементарным предикатам вроде <, = и >, существуют операции логической композиции, которые позволяют нам конструировать составные предикаты. Из них чаще всего используются такие:

• (and (e1) . . . (en))

Интерпретатор вычисляет выражения (e) по одному, слева направо. Если какое-нибудь из (e) дает ложное значение, значение всего выражения and — ложь, и остальные (e) не вычисляются. Если все (e) дают истинные значения, значением выражения and является значение последнего из них.

• (or (e1) . . . (en))

Интерпретатор вычисляет выражения (e) по одному, слева направо. Если какое-нибудь из (e) дает истинное значение, это значение возвращается как результат выражения or, а остальные (e) не вычисляются. Если все (e) оказываются ложными, значением выражения or является ложь.

• (not (e))

Значение выражения not — истина, если значение выражения (e) ложно, и ложь в противном случае

Заметим, что and и or — особые формы, а не процедуры, поскольку не обязательно вычисляются все подвыражения. Not — обычная процедура.

Как пример на использование этих конструкций, условие что число x находится в диапазоне 5 < x < 10, можно выразить как

(and (> x 5) (< x 10))

Другой пример: мы можем определить предикат, который проверяет, что одно число больше или равно другому, как

(define (>= x y)

(or (> x y) (= x y)))

или как

(define (>= x y)

(not (< x y)))