1.1.3 Вычисление комбинаций
Одна из наших целей в этой главе — выделить элементы процедурного мышления. Рассуждая в этом русле, примем во внимание, что интерпретатор, вычисляя значение комбинации, тоже следует процедуре:
Чтобы вычислить комбинацию, требуется:
- Вычислить все подвыражения комбинации.
- Применить процедуру, которая является значением самого левого подвыражения (оператора) к аргументам — значениям остальных подвыражений (операндов).
Даже в этом простом правиле видны несколько важных свойств процессов в целом. Прежде всего, заметим, что на первом шаге для того, чтобы провести процесс вычисления для комбинации, нужно сначала проделать процесс вычисления для каждого элемента комбинации. Таким образом, правило вычисления рекурсивно(recursive) по своей природе; это означает, что в качестве одного из своих шагов оно включает применение того же самого правила1.
Заметьте, какую краткость понятие рекурсии придает описанию того, что в случае комбинации с глубоким вложением выглядело бы как достаточно сложный процесс. Например, чтобы вычислить
(* (+ 2 (* 4 6))
(+ 3 5 7))
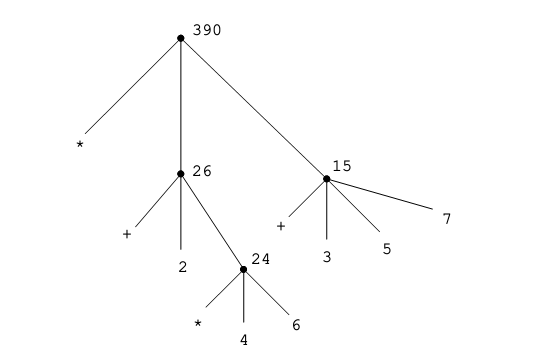
требуется применить правило вычисления к четырем различным комбинациям. Картину этого процесса можно получить, нарисовав комбинацию в виде дерева, как показано на рис. 1.1. Каждая комбинация представляется в виде вершины,а ее оператор и операнды — в виде ветвей, исходящих из этой вершины. Концевые вершины (то есть те, из которых не исходит ни одной ветви) представляют операторы или числа. Рассматривая вычисление как дерево, мы можем представить себе, что значения операндов распространяются от концевых вершин вверх и затем комбинируются на все более высоких уровнях. Впоследствии мы увидим, что рекурсия — это вообще очень мощный метод обработки иерархических, древовидных объектов. На самом деле форма правила вычисления «распространить значения наверх» является примером общего типа процессов, известного как накопление по дереву(tree accumulation).
Далее, заметим, что многократное применение первого шага приводит нас к такой точке, где нам нужно вычислять уже не комбинации, а элементарные выражения, а именно числовые константы, встроенные операторы или другие имена. С этими случаями мы справляемся, положив, что:
- значением числовых констант являются те числа, которые они называют;
- значением встроенных операторов являются последовательности машинных команд, которые выполняют соответствующие операции; и
- значением остальных имен являются те объекты, с которыми эти имена связаны в окружении.
Мы можем рассматривать второе правило как частный случай третьего, постановив, что символы вроде + и * тоже включены в глобальное окружение и связаны с последовательностями машинных команд, которые и есть их «значения». Главное здесь — это роль окружения при определении значения символов в выражениях. В таком диалоговом языке, как Лисп, не имеет смысла говорить о значении выражения, скажем, (+ x 1), не указывая никакой информации об окружении, которое дало бы значение символу x (и даже символу +). Как мы увидим в главе 3, общее понятие окружения, предоставляющего контекст, в котором происходит вычисление, будет играть важную роль в нашем понимании того, как выполняются программы.
Заметим, что рассмотренное нами правило вычисления не обрабатывает определений. Например, вычисление (define x 3) не означает применение define к двум аргументам, один из которых значение символа x, а другой равен 3, поскольку смысл define как раз и состоит в том, чтобы связать x со значением. (Таким образом, (definex 3) — не комбинация.)
Такие исключения из вышеописанного правила вычисления называются особыми формами (special forms). Define — пока что единственный встретившийся нам пример особой формы, но очень скоро мы познакомимся и с другими. У каждой особой формы свое собственное правило вычисления. Разные виды выражений (вместе со своими правилами вычисления) составляют синтаксис языка программирования. По сравнению с большинством языков программирования, у Лиспа очень простой синтаксис; а именно, правило вычисления для выражений может быть описано как очень простое общее правило плюс специальные правила для небольшого числа особых форм2.
1. Может показаться странным, что правило вычисления предписывает нам в качестве части первого шага вычислить самый левый элемент комбинации, — ведь до сих пор это мог быть только оператор вроде + или*, представляющий встроенную процедуру, например, сложение или умножение. Позже мы увидим, что полезно иметь возможность работать и с комбинациями, чьи операторы сами по себе являются составными выражениями. ↩
2. Особые синтаксические формы, которые представляют собой просто удобное альтернативное поверхностное представление для того, что можно выразить более унифицированным способом, иногда называют синтакси- ческим сахаром (syntactic sugar), используя выражение Питера Ландина. По сравнению с пользователями других языков, программистов на Лиспе, как правило, мало волнует синтаксический сахар. (Для контраста возьмите руководство по Паскалю и посмотрите, сколько места там уделяется описанию синтаксиса). Такое презрение к синтаксису отчасти происходит от гибкости Лиспа, позволяющего легко изменять поверхностный синтаксис, а отчасти из наблюдения, что многие «удобные» синтаксические конструкции, которые делают язык менее последовательным, приносят в конце концов больше вреда, чем пользы, когда программы становятся большими и сложными. По словам Алана Перлиса, «Синтаксический сахар вызывает рак точки с запятой». ↩