1.1.4 Составные процедуры
Мы нашли в Лиспе некоторые из тех элементов, которые должны присутствовать в любом мощном языке программирования:
- Числа и арифметические операции представляют собой элементарные данные и процедуры.
- Вложение комбинаций дает возможность комбинировать операции.
- Определения, которые связывают имена со значениями, дают ограниченные возможности абстракции.
Теперь мы узнаем об определениях процедур (procedure definitions) — значительно более мощном методе абстракции, с помощью которого составной операции можно дать имя и затем ссылаться на нее как на единое целое.
Для начала рассмотрим, как выразить понятие «возведения в квадрат». Можно сказать так: «Чтобы возвести что-нибудь в квадрат, нужно умножить его само на себя».
Вот как это выражается в нашем языке:
(define (square x) (* x x))
Это можно понимать так:
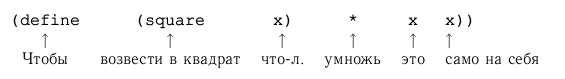
Здесь мы имеем составную процедуру (compound procedure), которой мы дали имя square. Эта процедура представляет операцию умножения чего-либо само на себя. Та вещь, которую нужно подвергнуть умножению, получает здесь имя x, которое играет туже роль, что в естественных языках играет местоимение. Вычисление этого определения создает составную процедуру и связывает ее с именем square1.
Общая форма определения процедуры такова:
(define ((имя) (формальные-параметры)) (тело))
(Имя) — это тот символ, с которым нужно связать в окружении определение процедуры. (Формальные-параметры) — это имена, которые в теле процедуры используются для отсылки к соответствующим аргументам процедуры. (Тело) — это выражение, которое вычислит результат применения процедуры, когда формальные параметры будут заменены аргументами, к которым процедура будет применяться2. (Имя) и (формальные-параметры) заключены в скобки, как это было бы при вызове определяемой процедуры.
Теперь, когда процедура square определена, мы можем ее использовать:
(square 21)
441
(square (+ 2 5))
49
(square (square 3))
81
Кроме того, мы можем использовать square при определении других процедур. Например, x 2 + y 2 можно записать как
(+ (square x) (square y)))
Легко можно определить процедуру sum-of-squares, которая, получая в качестве аргументов два числа, дает в результате сумму их квадратов:
(define (sum-of-squares x y)
(+ (square x) (square y)))
(sum-of-squares 3 4)
25
Теперь и sum-of-squares мы можем использовать как строительный блок при дальнейшем определении процедур:
(define (f a)
(sum-of-squares (+ a 1) (* a 2)))
(f 5)
136
Составные процедуры используются точно так же, как элементарные. В самом деле, глядя на приведенное выше определение sum-of-squares, невозможно выяснить, была ли square встроена в интерпретатор, подобно + и *, или ее определили как составную процедуру.
1. Заметьте, что здесь присутствуют две различные операции: мы создаем процедуру, и мы даем ей имя square. Возможно, и на самом деле даже важно, разделить эти два понятия: создавать процедуры, никак их не называя, и давать имена процедурам, уже созданным заранее. Мы увидим, как это делается, в разделе 1.3.2. ↩
2. В более общем случае тело процедуры может быть последовательностью выражений. В этом случае интерпретатор вычисляет по очереди все выражения в этой последовательности и возвращает в качестве значения применения процедуры значение последнего выражения. ↩